• Un site web fait par un prof de math sans math... ça commençait à devenir grave.
  • Comme il existe de nombreux sites très complets sur le sujet je n'en éprouvais pas non plus le besoin.
  • Pour ceux qui veulent s'instruire, quelques liens sont présents sur la page.
  • Vous retrouverez sur ces sites certaines des citations ou histoires.
  • Je n'ai rien inventé, j'ai juste compilé des curiosités lues ou entendues. Rendons à César...
  • Une partie de ce qui suit provient de ces sites ou de mes amis, collègues etc... merci à eux tous.
  • je me suis juste penché sur "l'aspect comique" de la "chose mathématique" et des mathématiciens en particulier.


Commentaires, suggestions ou contributions...











Préambule.
Avant chaque histoire, j'ai noté le niveau et connaissances en math nécessaire à sa compréhension.
l'échelle va du niveau zéro à post bac...
Histoire N°1. "Accessible à tous".

Trois employés d'une société (en ingénieur, un physicien et un mathématicien) passent une nuit dans un hôtel.
Histoire N°2. "Accessible à tous".

Trois hommes se trouvent dans un ballon à air chaud. Bientôt, les voilà perdus quelque part au milieu d'un canyon.
L'un des trois hommes déclare : "J'ai une idée. Nous pourrions appeler à l'aide, et l'écho portera nos voix au loin."
Ainsi, il bondit hors de la nacelle, et cria "Hellllloooooooooooo! Où sommes-nous ?" (ils entendent l'écho plusieurs fois)...
15 minutes après, ils entendent une voix portée par l'écho : "Hellllloooooooooooo! Vous êtes perdus !!" Puis plus rien...
L'un des trois hommes s'exprima alors : "Hum ! Ce devait être un mathématicien..."
Intrigué, un des autres hommes lui demanda : "Pourquoi dis-tu ça ?"
"Pour trois raisons. (1) Il a mis longtemps pour répondre, (2) il avait absolument raison, et (3) sa réponse était absolument inutile."
Histoire N°3. "Accessible à tous".

Un biologiste, un statisticien et un mathématicien font un safari en Afrique. Ils se promènent en Jeep, s'arrêtent, et scrutent l'horizon avec leurs jumelles.
Histoire N°4. "Accessible à tous".

Un médecin, un avocat et un mathématicien discutent les avantages et les inconvénients d'avoir une femme ou une amante.
Histoire N°5. "Minimum bac scientifique : notions sur les primitives".

Deux mathématiciens sont dans un bar, discourant de la vie en général...
Le premier dit au second que la plupart des gens ne connaissent pas grand chose aux maths qu'ils sont ignares... Pour lui les hommes sont des barbares en puissances dont la soif de pouvoir et d'argent est infinie.
Le second réfute cette thèse , et affirme que la plupart des gens peuvent manier des notions de base des maths. Il est optimiste, pour lui l'homme est bon , généreux etc...
Le premier mathématicien (le pessimiste donc) va aux toilettes, et pendant son absence, le second (optimiste si vous suivez) appelle la serveuse, une jolie blonde aux yeux bleus dont la tenue légère, les seins opulents ainsi qu'un décolleté plongeant lui donne confiance en la race humaine, du moins sa composante féminine...
Il lui dit que dans quelques minutes, lorsque son ami sera revenu, il va l'appeler pour lui poser une question....
Tout ce qu'elle aura à faire, ce sera de répondre : "un tiers de x cube".
Elle répète (un peu niaisement on peut le dire...) " un tiers de iks cub ? " Il répète, convaincant "un tiers de x cube".
Elle: "un tiers de ix cub ?" Oui, c'est ça, dit-il, priant le ciel pour que son odieux stratagème fonctionne...
Elle accepte et s'en vaconcentrée en murmurant longuement "un tiers deix cub..."
Le premier homme revient et le second lui propose un pari pour prouver ces dires, que beaucoup de gens s'y connaissent en maths. (vous commencez, cher lecteur, à comprendre the big ruse...)
Il lui dit qu'il va appeler une serveuse, jolie (donc a priori très c...) et lui demander une primitive.
Le premier accepte le pari, en rigolant, sûr de gagner...
Le second appelle la serveuse et lui demande : "Que vaudrait la primitive de x au carré ?"
La serveuse répond avec un sourire : "un tiers de x cube..."
Stupéfaction chez notre mathématicien pessimiste... son regard trahit mal son étonnement...
La serveuse s'éloigne... se retourne... et dit par-dessus son épaule à nos deux compères : " enfin, à une constante près..."
Histoire N°6. "Minimum bac scientifique : notions sur la fonction exponentielle."

Un mathématicien fou monte dans un bus et se met à menacer tout le monde : " Je vais vous intégrer ! Je vais vous dériver !!".
Tout le monde est effrayé et se sauve, sauf une jeune dame qui reste tranquille.
Le mathématicien fou arrive vers elle et lui dit : " Tu n'as pas peur ? Je vais t'intégrer ! Je vais te dériver !!".
"Non" répond la jeune dame : "je n'ai pas peur, je suis la fonction exponentielle"
Histoire N°7. "Minimum bac scientifique : notions sur la fonction exponentielle et analyse."

Une fonction constante et la fonction qui à "x" associe "exp(x)" ("par abus de langage" on l'appellera exp(x) ) marchent tranquillement dans la rue (je sais c'est pas réaliste mais les complexes au premier abord ça ne l'est pas plus...)
Soudain la fonction constante aperçoit un opérateur différentiel qui approche. Elle se sauve.
exp(x) la rattrape et lui demande ce qui lui prend. " Tu ne te rends pas compte ! Si l'opérateur différentiel me rencontre, il me dérivera et il ne restera rien de moi... !"
"Ah ! Ah!", dit exp(x), "il ne m'inquiète pas, MOI, je suis e puissance x !". Et elle poursuivit sa route tranquille fière les cheveux au vent..
Évidemment, au bout de quelques km, elle rencontre l'opérateur différentiel en question.
exp(x) se la jouant un peu beaucoup... "Salut, je suis exp(x) !"
L'opérateur différentiel mi-rieur mi-moqueur : "Salut, je suis d/dy..."
Histoire N°8. "Accessible à tous"

Un physicien et un mathématicien sont assis. Soudain, la machine à café prend feu...
Le physicien se lève, saisit un seau, court le remplir et éteint le feu.
Le lendemain, alors qu'ils sont assis au même endroit, la machine à café prends de nouveau feu.
Le mathématicien saisit le seau, le tend au physicien et ramène ainsi le problème à un problème précédemment résolu.
Histoire N°9. "Accessible à tous"

Un mathématicien, un chimiste et un physicien assistent à la conférence d'un éminent physicien concernant les théories de Kulza-Klein sur les processus physiques intervenant dans les espaces de dimension 9.
Au bout de 2 mn le chimiste la tête entre les mains abandonne toute idée de suivre cette conférence. Tout cela le dépasse et franchement il aurait dû aller voir le P.S.G. au Parc des Princes. Le foot, c'est relaxant non ?
Le physicien, lui, suit l'exposé. Teigneux et opiniâtre, il s'accroche, transpire, prend des notes. Il est concentré comme jamais. Rouge il alimente au maximum son cerveau en oxygène pour comprendre la théorie de kulza-klein dans ces fameux espaces de dimension 9.
Le mathématicien est assis et semble apprécier la conférence. Il a le sourire au lèvre de celui qui comprend ce qui se passe. Tout en écoutant, il lit un peu le journal "L'Equipe" pour se tenir au courant des derniers résultats du foot (ben oui les matheux aiment aussi le foot...). Il se permet au cours de la séance, de poser une ou deux questions qui font leurs effets puisque les sommités présentes les notent religieusement, absorbées dans de ténébreuses pensées...
Nos trois amis se retrouvent au café. Le chimiste déclare avoir complètement décroché dès le début. Et toi ? dit-il au physicien, t'as pigé ?
Ben, oui mais j'en ai vraiment ch... j'étais à 400% de mes possibilités... les deux se tournent vers le mathématicien.
Comment tu as fait pour comprendre tout ça ? On a eu beaucoup de mal à visualiser le processus tout ça dans cette foutue dimension neuf. C'est quoi ton truc ?
Le mathématicien : " C'est simple. D'abord vous visualisez le processus en dimension n quelconque, et ensuite il suffit de prendre n=9."

Histoire N°10. "Accessible à tous"

c'est exponenetielle et logarithme en base e qui vont au restaurant . Qui est-ce qui paye? c'est expônentielle parce que logarithme ne paie rien... ouarf !!!!
Retour au menu de la page.






Voici quelques très bons et beaux sites sur les mathématiques.
Retour au menu de la page.





Démonstration : tous les triangles sont isocèles.

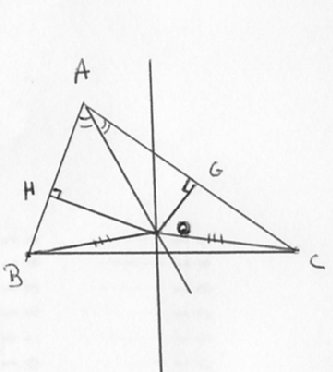
Soit O le point d'intersection de la bissectrice de l'angle  et de la médiatrice de [BC]. Considérons H et G les projetés orthogonaux respectifs de O sur les droites (AB) et (AC). Regardez la figure. Même si elle n'est pas géniale, je l'avoue humblement :-((( . Honte à moi sur ce coup ! Mais ne nous égarons pas dans des futilités... je reprends donc.
Remarque : y'a de quoi méditer une fois que l'on a vu l'entourloupe...

Paradoxe de Tarsky.

Le but du jeu est de démontrer que dans une boîte de crayons de couleur... tous les crayons sont de la même couleur. Dingue non ?
Pour ça, on va utiliser un outil vachetement puissant, issu de la pure abstraction de l'esprit humain (c'est dire si c'est méga-giga-terra puissant comme dirait mon fils Arthur), je veux nommer ici "le principe de la récurrence". Attention à la suite donc... (jeu de mots inévitable ).

Tout entier positif est intéressant.

Supposons le contraire c'est à dire qu'il y ait des entiers qui ne le soient pas. Alors il y a un plus petit élément parmi ces entiers non-intéressants. Faut connaître un nminimum de choses sur l'ensemble des entiers positifs, mais bon intuitivement c'est logique.
Du coup cet entier est drôlement intéressant ! Ben oui il est même très très intéressant...
Bref on voit surgir la contradiction , d'où l'énoncé.

Tous les nombres impairs supérieurs à 2 sont premiers.

Il s'agit presque d'une histoire "drôle".
En voici les démonstrations de différentes personnes.
Retour au menu de la page.
Du nouveau bientôt...